S’adapter au contexte: les instructions conditionnelles

S’adapter au contexte: les instructions conditionnelles#

Motivation : rôle des structures de contrôle#

Indication

Rappel Nous avons vu que les instructions d’un programme sont exécutées de manière séquentielle (les unes après les autres), dans l’ordre où elles sont données, comme dans l’exemple suivant.

Exemple

debut()
droite()
avance()
prend()
gauche()
avance()
pose()
droite()
avance()
gauche()
avance()
avance()
droite()
ouvre()
../_images/laby0.png

Cependant, on a souvent besoin de rompre cette exécution séquentielle :

  • Soit pour s”adapter au contexte :

    Le labyrinthe 3a avec petite et grande toile Le labyrinthe 3a avec petite et grande toile

  • Soit pour répéter des instructions :

    Un labyrinthe tout en longueur

Pour cela, nous avons besoin des structures de contrôle. Dans cette feuille, nous allons explorer comment s’adapter au contexte avec les instructions conditionnelles. Ultérieurement, nous verrons comment répéter des instructions.

Instructions conditionnelles#

Introduction#

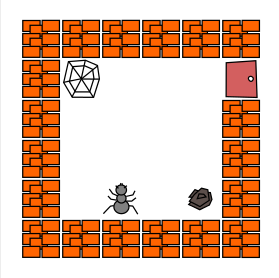
Le principe général est que, en fonction d’une condition, on va exécuter ou non certaines instructions. Voyons cela sur le premier labyrinthe ci-dessus que vous avez déjà croisé :

from laby.global_fr import *
Laby(niveau="3a")

Exécutez plusieurs fois la cellule suivante :

debut()
droite()
avance()
gauche()

Vous aurez noté qu’une fois la fourmi arrivée à cet endroit du labyrinthe, elle fait, selon les cas, face à une grande toile d’araignée (mortelle!) ou une petite. Elle doit donc agir différemment selon ce contexte.

  1. Si elle fait face à une grande toile d’araignée, elle doit faire demi-tour pour passer par l’autre côté du labyrinthe.

  2. Sinon elle fait face à une petite toile d’araignée qu’elle peut traverser sans danger.

Voilà comment cela peut s’écrire :

Laby(niveau="3a")

debut()
droite()
avance()
gauche()

if regarde() == Toile:
    gauche()
    avance()
    avance()
    droite()
    avance()
    avance()
    droite()
    avance()
    gauche()
else:
    avance()
    avance()
    gauche()
    avance()
    droite()

ouvre()

Les instructions conditionnelles#

Nous allons maintenant introduire formellement les instructions conditionnelles, et tout d’abord spécifier comment regrouper plusieurs instructions ensemble comme ci-dessus (et comme apperçu précédemment avec les fonctions.; cela se fait en Python à l’aide de l’indentation :

Définition : Bloc d’instructions

Un bloc d’instructions (code block) est une suite d’une ou plusieurs instructions à exécuter successivement. Il est délimité par son indentation (par convention quatre espaces de plus que le code environnant) ainsi que par un “:” sur la ligne qui précède :

    ...:

        instruction 1
        instruction 2
        ...
        instruction n

    ...

Nous pouvons maintenant définir les instructions conditionnelles simples et alternatives.

À faire

ajouter un definiendum

Définition : Instruction conditionnelle simple : «si … alors …»

Syntaxe :

if condition:
    bloc d instructions

Sémantique

  1. Évaluation de la condition

  2. Si sa valeur est vraie, exécution du bloc d’instructions

Exemple

if regarde() == Toile:     # Au secours, fuyons!
    gauche()
    gauche()

Définition : Instruction conditionnelle alternative : «si … alors … sinon …»

Syntaxe

if condition:
    bloc d instructions 1
else:
    bloc d instructions 2

Sémantique

  1. Évaluation de la condition

  2. Si sa valeur est «Vrai», exécution du bloc d’instructions 1

  3. Si sa valeur est «Faux», exécution du bloc d’instructions 2

Exemple

if regarde() == Toile:    # Au secours, fuyons!
    gauche()
    gauche()
else:                     # Tout va bien
    avance()

Exemple : Calcul du maximum et du minimum de deux nombres

Les quatre cellules ci-dessous illustrent le calcul du maximum et du minimum des deux nombres contenus dans des variables x et y.

x = 3              # Les entrées
y = 5

if ( x > y ):
    maximum = x
    minimum = y
else:
    maximum = y
    minimum = x

minimum

3

maximum

5

Exercice

  1. Testez le code suivant avec plusieurs valeurs de \(a\) et \(b\). Que fait-il ?

a = 10
b = 5

if a > b:
    print(a)
else:
    print(b)

10

Solution

Il calcule le maximum entre a et b et l’affiche.

Exercice

Dans cet exercice, vous allez utiliser la fonction max ci-dessous pour calculer le maximum de deux nombres, trois nombres et quatre nombres.

def max(a, b):
    if a > b:
        return a
    else:
        return b

n1 = -2
n2 = 6
n3 = 0
n4 = 7

Exercice (suite)

  1. Calculez le max de n1 et n2 (en utilisant la fonction max) :

### BEGIN SOLUTION
max(n1, n2)
### END SOLUTION

6

Exercice (suite)

  1. Calculez le max de n1, n2 et n3 Indication: utilisez deux fois la fonction max.

### BEGIN SOLUTION
max(n1, max(n2, n3))
### END SOLUTION

6

Exercice (suite)

  1. Calculez le max de n1, n2, n3 et n4 (toujours en utilisant la fonction max)

### BEGIN SOLUTION
max(n1, max(n2, max(n3, n4)))
### END SOLUTION

7

Exercice (suite)

  1. Changez les valeurs de n1, n2, n3 et n4 ci-dessus, re-exécutez les cellules et vérifiez les résultats.

Rappel : Les exercices précédés d’un ♣ sont plus difficiles et facultatifs. Il n’est pas nécessaire de les maîtriser pour passer à la suite.

Exercice (suite)

  1. ♣ Écrivez une fonction max4 prenant quatre entiers et calculant leur max :

### BEGIN SOLUTION
def max4(a, b, c, d):
    return max(a, max(b, max(c, d)))
### END SOLUTION

Exercice (suite)

  1. ♣ Utilisez votre fonction max4 pour calculer le max de n1, n2, n3 et n4 :

### BEGIN SOLUTION
max4(n1, n2, n3, n4)
### END SOLUTION

7

Exercice

  1. Complétez la fonction min ci-dessous. Indication consultez l’exemple de la fonction max plus haut et adaptez le.

def min(a, b):
    ### BEGIN SOLUTION
    if ( a < b ):
        return a
    else:
        return b
    ### END SOLUTION

Exercice (suite)

  1. Essayez-la sur l’exemple suivant:

min(2,3)

2

Exercice (suite)

  1. Essayez-la sur un exemple de votre choix :

### BEGIN SOLUTION
min(6, 0)
### END SOLUTION

0

Exercice (suite)

  1. Vérifiez que tous les tests qui suivent ont bien la valeur true :

min(5, 10) == 5

True

min(6, -2) == -2

True

min(-3, -4) == -4

True

min(5, min(-3, 8)) == -3

True

Exercice (suite)

  1. La cellule suivante contient des tests automatisés; nous reviendrons dessus plus en détails par la suite; exécutez la cellule et vérifiez qu’il n’y a pas de message d’erreur.

assert( min(5, 10) ==  5 )
assert( min(6, -2) == -2 )
assert( min(2,  2) ==  2 )

Exercice

  1. Complétez la fonction abs ci-dessous qui calcule la valeur absolue d’un nombre :

def abs(a):
    ### BEGIN SOLUTION
    if ( a < 0 ):
        return -a
    else:
        return a
    ### END SOLUTION

Exercice (suite)

  1. Utilisez cette fonction pour calculer la valeur absolue de -2.5 et vérifiez le résultat :

### BEGIN SOLUTION
abs(-2.5)
### END SOLUTION

2.5

Exercice (suite)

  1. Vérifiez que les tests qui suivent ont bien la valeur True :

abs(-5.1) == 5.1

True

abs(2.3) == 2.3

True

abs(-3.4) == 3.4

True

Exercice (suite)

  1. Vérifiez que les tests automatisés ci-dessous ne produisent pas d’erreur :

assert abs( 0.0) == 0.0
assert abs( 2.3) == 2.3
assert abs(-3.4) == 3.4

Nous allons maintenant voir comment traiter des contextes avec plus de deux cas.

Définition : Instruction conditionnelle filée : «si … alors … sinon si … alors sinon …»

Syntaxe

if condition1:
    bloc d instructions 1
elif condition2:
    bloc d instructions 2
else:
    bloc d instructions 3

Sémantique

Le code ci-dessus est strictement équivalent à (mais plus lisible que) :

if condition1:
    bloc d instructions 1
else:
    if condition2:
        bloc d instructions 2
    else:
        bloc d instructions 3

Il peut y avoir autant de clauses elif que nécessaire.

Exercice

Complétez la fonction frais_de_livraison ci-dessous qui prend en paramètre une distance en kilomètres et renvoie le montant des frais de livraison en fonction de cette distance selon les règles suivantes :

  • Si la distance est inférieure ou égale à 5 km, les frais de livraison sont de 5 €.

  • Si la distance est comprise entre 5 km (exclus) et 20 km (inclus), les frais de livraison sont de 10 €.

  • Si la distance est supérieure à 20 km, les frais de livraison sont de 15 €.

def frais_de_livraison(distance):
    ### BEGIN SOLUTION
    if distance <= 5:
        return 5
    elif distance <= 20:
        return 10
    else:
        return 15
    ### END SOLUTION

assert frais_de_livraison(3) == 5
assert frais_de_livraison(10) == 10
assert frais_de_livraison(30) == 15

Conclusion#

Dans cette feuille, nous avons vu comment utiliser des instructions conditionnelles simples, alternatives ou filées pour adapter le comportement du programme en fonction du contexte, selon le nombre de cas à traiter.

Avant de passer à la suite, nous vous proposons quelques exercices d’entraînement et de révisions autocorrigés.

import glob, os
from jupylates import Exerciser
os.chdir("../exercices")
Exerciser(glob.glob('conditions/*.md'))
Contenu