Practice: weather data

This section will compute statistics and observe trends in monthly weather data in the period 1951-2023. We use real measurements from Météo-France that are available for any region in France ( https://meteo.data.gouv.fr/datasets/ ). We simplified the task by creating the data file chamonix_weather_data_1951-2023.csv that contains data from one of Chamonix observatories. You can use the code written previously in the previous section where you build a weather station.

The following exercises can be either solved using only native python tools, or using specialized libraries to handle csv data. The former is better to learn python, but the latter is a lot more efficient.

Load the data

The main difference with the previous exercises is that the files are getting bigger and treating them by hand is not a good way to proceed anymore. Still, since we are dealing with a text file, it is a good idea to open the file and check the content. The first line gives the name of each column, where NOM_USUEL is the location name (only Chamonix in our case), AAAAMM is the date, RR is the rain (more precisely: cumul mensuel des hauteurs de précipitation (en mm et 1/10)), TM the average temperature.

Exercise 30

Read the file chamonix_weather_data_1951-2023.csv in ../../common/data_read_files/ and load the data in the structure of your choice. You can use a structure defined elsewhere. There is some missing data points in the serie which you can discard.

You can use functions:

def load_data(path, separator=";"):
    """Loading the data from a file in a single dictionary"""
    pass


path = "../../common/data_read_files/chamonix_weather_data_1950-2023.csv"
station = load_data(path)

or classes:

from typing import Self


class WeatherStation:
    """A weather station that holds wind and temperature"""

    def __init__(self):
        """initialize the weather station with empty values"""
        pass

    @classmethod
    def from_csv(self, path: str, name: str, sep=";") -> Self:
        """loads a filename using the fields
            NOM_USUEL       : nom usuel du poste
            AAAAMM          : mois
            RR              : cumul mensuel des hauteurs de précipitation (en mm et 1/10)
            TM              : moyenne mensuelle des (TN+TX)/2 quotidiennes (en °C et 1/10)
        raise RuntimeError if import fails
        :path: str
        :returns: None
        """
        pass

Solution to Exercise 30

We present two solutions, first one with dictionaries

def load_data(path, separator=";", nb_fields=4):
    """Loading the data from a file in a single dictionary"""

    station = {
        "location": [],
        "rain": [],
        "temperatures": [],
        "dates": [],
    }
    with open(path) as f:
        f.readline()
        for line in f:
            # strip the end of line
            line = line.strip("\n")
            ch = line.split(separator)

            place = ch[0]
            date = ch[1]

            station["location"].append(place)
            station["dates"].append(date)

            try:  # in case of missing data (or corrupt), discard the full line
                rain = float(ch[2])
                temperature = float(ch[3])
            except ValueError:
                # save data
                station["rain"].append(np.nan)
                station["temperatures"].append(np.nan)

            # save data
            station["rain"].append(rain)
            station["temperatures"].append(temperature)

    return station


path = f"../common/data_read_files/chamonix_weather_data_1951-2023.csv"
station = load_data(path)

and a second with classes

import numpy as np
import pandas as pd
from pathlib import Path


class WeatherStation:
    """A weather station that holds weather data, namely

    - dates
    - location
    - rain
    - temperatures
    """

    def __init__(self, name: str, dates, location, rain, temperatures):
        """initialize the weather station."""
        self.name = name
        self.dates = dates
        self.location = location
        self.rain = rain
        self.temperatures = temperatures

    @classmethod
    def from_csv(cls, filename: str, name: str, sep=";") -> Self:
        """
        loads a csv filename using the fields
            NOM_USUEL       : nom usuel du poste
            AAAAMM          : mois
            RR              : cumul mensuel des hauteurs de précipitation (en mm et 1/10)
            TM              : moyenne mensuelle des (TN+TX)/2 quotidiennes (en °C et 1/10)
        raise RuntimeError if import fails
        :filename: str|Path
        :returns: None
        """
        df = pd.read_csv(filename, sep=sep)

        # change date to a more convenient format
        df["dates"] = pd.to_datetime(df.AAAAMM, format="%Y%m")

        location = df["NOM_USUEL"]
        rain = df["RR"]
        temperatures = df["TM"]

        return WeatherStation(name, df["dates"], location, rain, temperatures)


path = "../common/data_read_files/chamonix_weather_data_1951-2023.csv"
chamonix = WeatherStation.from_csv(path, "Chamonix")

Compute statistics

Exercise 31

In this part, you will access the database you wrote previously and compute statistics from the data. Specifically

• Compute the average temperature during the full period 1950-2023 and its standard deviation

• Compute the average rainfall in June in the full period

• Compute the average temperature when it is raining more than 100 mm during the month

Note: When computing averages, we consider each month to weight the same (February has the same weight despite having less days).

Solution to Exercise 31

# convert numerical data to numpy arrays
for key in ["rain", "temperatures"]:
    station["rain"] = np.array(station["rain"])
    station["temperatures"] = np.array(station["temperatures"])

# Check that there is no nans values
nans_mask = np.isnan(station["temperatures"])
print("invalid values:", np.sum(nans_mask))

# compute average on all values
avg_temp = np.mean(station["temperatures"])
sigma_temp = np.std(station["temperatures"])
print(f"Average temperature (1951-2023): {avg_temp:.2f} +/- {sigma_temp:.2f} °C")

# slicing does not work (i.e. station['rain'][5::12]) if there are missing elements!
# Instead, one should look for dates that finish with 6
june_rain = station["rain"][5::12]  # take every 12 elements, starting in june
print(f"Average rain in june (1951-2023): {np.mean(june_rain):.2f} mm")

# find indices when rain is superior to 100mm
heavy_rain_months = station["rain"] > 100
temp_when_raining = np.mean(station["temperatures"][heavy_rain_months])
print(f"Average temp in rainy months (1951-2023): {temp_when_raining:.2f} °C")

invalid values: 0
Average temperature (1951-2023): 7.12 +/- 6.91 °C
Average rain in june (1951-2023): 122.78 mm
Average temp in rainy months (1951-2023): 8.04 °C

With the oriented object and pandas

# compute average on all values but nans
avg_temp = chamonix.temperatures.mean()
sigma_temp = chamonix.temperatures.std()
print(f"Average temperature (1951-2023): {avg_temp:.2f} +/- {sigma_temp:.2f} °C")

# use pandas datetime to get something clearer than Numpy
june_rain = chamonix.rain[chamonix.dates.dt.month == 6]
print(f"Average rain in june (1951-2023): {np.mean(june_rain):.2f} mm")

# find indices when rain is superior to 100mm
heavy_rain_months = chamonix.rain > 100
temp_when_raining = chamonix.temperatures[heavy_rain_months].mean()
print(f"Average temp in rainy months (1951-2023): {temp_when_raining:.2f} °C")

Average temperature (1951-2023): 7.12 +/- 6.91 °C
Average rain in june (1951-2023): 122.78 mm
Average temp in rainy months (1951-2023): 8.04 °C

Climate evolution

We now turn to the more interesting part, we compute how temperatures increased in Chamonix. Then we model the temperatures to make a prediction for 2050.

Exercise 32

We model the temperature evolution in the simplest way possible and assume that the temperature increase linearly.

• Use numerical dates (for instance ‘2020-06’ should be 2020.5)

• Plot the temperatures as a function of time.

Approximate the temperature \(T\) as a function of time \(t\), \(T(t) = a * t + b\). Find the two parameters \(a\) and \(b\), resp. the slope and intercept, that provide the best fit to the data. We recommend to use the function scipy.optimize.curve_fit.

from scipy.optimize import curve_fit


def linear(dates, slope, intercept):
    return slope * dates + intercept


# fit the model with curve_fit
pass

Other options such as scikit_learn or solving ordinary least square is also possible, but is more involved mathematically. Control that the model follows the data by plotting the model and the data on the same plot. Print the change in degrees per century and the average temperature predicted in 2050.

Solution to Exercise 32

For both approaches, we need to convert the dates to numerical values

# convert dates to numerical values
years = [int(d[:4]) for d in station["dates"]]  # years correspond to 4 first characters
months = [
    int(d[4:]) for d in station["dates"]
]  # months correspond to 2 last characters
station["numerical_dates"] = np.array(years) + (np.array(months) - 1) / 12

And for pandas

# convert dates to numerical values
numerical_dates = chamonix.dates.dt.year + (chamonix.dates.dt.month - 1) / 12
temperatures = chamonix.temperatures

The rest of the exercise can be done in the same way

import matplotlib.pyplot as plt

fig, ax = plt.subplots()

ax.set_xlabel("Years")
ax.set_ylabel("Temp (°C)")
ax.plot(numerical_dates, temperatures);

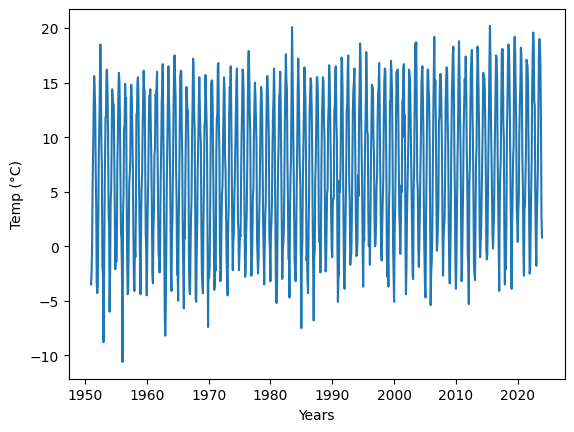
from scipy.optimize import curve_fit


def linear(dates, slope, intercept):
    return slope * dates + intercept


# we fit the model
opt_params, pcov = curve_fit(
    linear,
    numerical_dates,
    temperatures,
)
slope, intercept = opt_params

# important, test if the model fit the data
# since this is a line, we only need two points

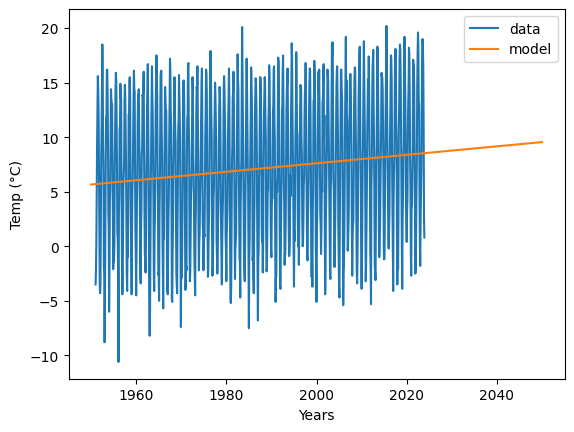
fig, ax = plt.subplots()


ax.plot(numerical_dates, temperatures, label="data")  # plot the data for reference
times = [1950, 2050]
temps_model = [slope * time + intercept for time in times]
ax.set_xlabel("Years")
ax.set_ylabel("Temp (°C)")
ax.plot(times, temps_model, label="model")
plt.legend()

print(f"temperature change {slope * 100:.2f} °C / 100 year")
print(f"Average temperature in 2050 {temps_model[1]:.2f} °C")

temperature change 3.89 °C / 100 year
Average temperature in 2050 9.55 °C

Final comment: The exercises could be solved with either pandas or numpy. However the two librairies have different scopes. To read CSV files, compute means, or handle dates pandas offer a simpler interface. However to perform more complex mathematical operations such as linear algebra operations, numpy is a better choice. Furthermore, numpy arrays are handled by a variety of other librairies (e.g. scipy). In practice, you can of course use both librairies, depending on the task. If you want to redo the exercise with other stations, which will likely have missing data, the simplest way is to use pandas.